If asked to name the key concepts of the common core, I would choose (a) the properties of operations, (b) the relationship between addition and subtraction and (c) the relationship between multiplication and division.
What? I better dust off my old high school algebra book!
Actually, these concepts are not as difficult as they initially sound. However, students do need to gain a complete mastery of them as they are used throughout the Common Core Standards.
The following are definitions and some examples of their use:
The Properties of Operations
The term “properties of operations” refers to the commutative, associative and distributive properties.
The Commutative Property of Addition
It does not matter in what order numbers are added. The numbers can be reversed and the sum (answer) will always be the same.
7 + 8 = 15
8 + 7 = 15
The Associative Property of Addition
Given 3 or more numbers to add together, it does not matter how the numbers are grouped or added. The sum (answer) will always be the same.
4 + (6 + 10) = 4 + 16 = 20
(4 + 6) + 10 = 10 + 10 = 20
The Commutative Property of Multiplication
It does not matter in what order numbers are multiplied. The factors can be reversed and the product (answer) will always be the same.
8 x 7 = 56
7 x 8 = 56
The Associative Property of Multiplication
Given 3 or more numbers to multiply together, it does not matter how the numbers are grouped or multiplied. The product (answer) will always be the same.
3 x (7 x 10) = 3 x 70 = 210
(3 x 7) x 10 = 21 x 10 = 210
Students do not have to know the names for these properties, but should be able to demonstrate an understanding of the concepts by drawing pictures or by arranging “manipulatives” such as pennies. To demonstrate an understanding of the commutative property of addition, a student could draw the following pictures to show that 7 + 8 and 8 + 7 both equal 15.
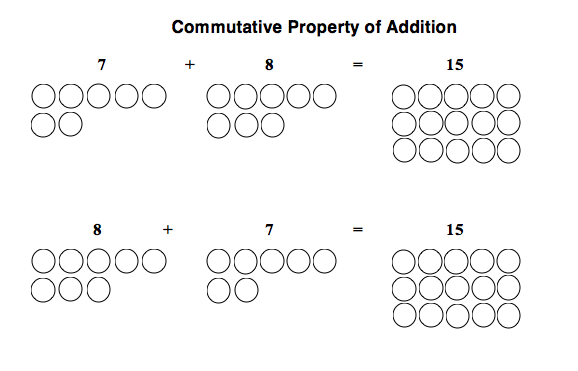 To demonstrate an understanding of the commutative property of multiplication, a student could draw the following arrays to show that 8 rows of 7 are the same as 7 rows of 8.
To demonstrate an understanding of the commutative property of multiplication, a student could draw the following arrays to show that 8 rows of 7 are the same as 7 rows of 8.
The Distributive Property of Multiplication
Third grade students begin to use the distributive property as a strategy to assist them in learning basic multiplication facts. For example, to find the more difficult fact of 7 x 8, students might break the 8 into the two simpler numbers of (5 + 3). The 7 is then multiplied or “distributed” to each number inside of the parentheses.
Example: 7 x (5 + 3) = (7 x 5) + (7 x 3)
To find the solution, students would use the following steps:
Step 1: Multiply: (7 x 5) = 35
Step 2: Multiply: (7 x 3) = 21
Step 3: Add: 35 + 21 = 56
The Use of Area Models
Students will draw “models” or representations of multiplication problems to assist them with their learning. The area model drawn on graph paper below shows the use of the distributive property to find 7 x 8 = 56.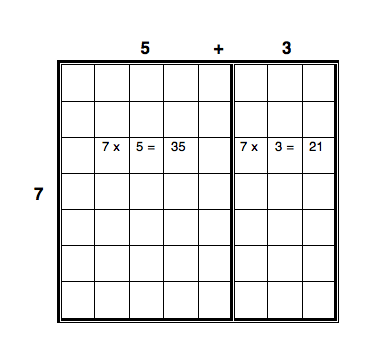
The Use of the Distributive Property in the Fourth and Fifth Grades
Fourth grade students will multiply more complex whole numbers using the distributive property. Fifth grade students will also use the property to multiply fractions, mixed numbers and decimals. Students will continue to draw area models to represent their solutions.
An Example of a Fourth Grade Multiplication Problem
Example: Solve 3 x 127. Use the distributive property of multiplication.
Step 1: Break 127 into (100 + 20 + 7)
Step 2: Create the expression: (3 x 100) + (3 x 20) + (3 x 7)
Step 3: Solve the expression:
(a) Multiply: (3 x 100) = 300
(b) Multiply: (3 x 20) = 60
(c) Multiply: (3 x 7) = 21
(d) Add: 300 + 60 + 21 = 381
 An Example of a Fifth Grade Multiplication Problem
An Example of a Fifth Grade Multiplication Problem
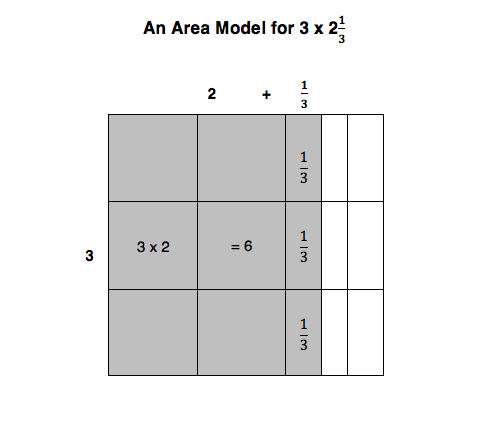
Example: Solve 3 x 2 . Use the distributive property of multiplication.
Step 1: Break 2 into 2 +
Step 2: Create the expression: (3 x 2) + (3 x )
Step 3: Solve the expression:
(a) Multiply: ( 3 x 2 ) = 6
(b) Multiply: ( 3 x ) =
(c) Add: 6 + = 6 + 1 = 7
 The Relationship between Addition and Subtraction
The Relationship between Addition and Subtraction
This sounds confusing, but all it means is that addition and subtraction have an inverse or opposite relationship.
For example: “If I know that 7 + 8 = 15, I also know that 15 – 7 = 8.”
Counting Up to Solve a Subtraction Problem
Because of this opposite relationship, students can count up to solve a subtraction problem.
Example: Find a solution for 87 – 42. Use the relationship between addition and subtraction.
Step 1: Turn the problem into an unknown addition problem.
42 + ![]() = 87
= 87
Step 2: Solve for ![]() by counting up.
by counting up.
42 + 40 = 82
82 + 5 = 87
Step 3: Combine the numbers that were added on: 40 + 5 = 45
![]() = 45
= 45
The Relationship between Multiplication and Division
Similar to addition and subtraction, the relationship between multiplication and division is an inverse or opposite relationship.
For example: “If I know that 7 x 8 = 56, I also know that 56 ÷ 7 = 8.”
Because the Common Core emphasizes multiplication over division, this inverse relationship is utilized throughout the Standards.
Finally, a few words about Visual Fraction Models
This is a term used throughout the Common Core that simply means pictures, number lines, and area models. Most of the fraction standards require that students draw a “model” or representation of their solutions. Visual fraction models can be used to show the addition, subtraction, multiplication, and division of fractions. Review my Lesson Plans for the individual standards listed below to help your student master these important skills.




